When does Delsarte’s bound hold?

Philippe Delsarte (An algebraic approach to the association schemes of coding theory. Philips Res. Rep. Suppl., 10:vi+97, 1973) generalised the “MacWilliams transform” of coding theory to the theory of association schemes, and there have been numerous powerful applications of this object, particulary in finding the maximum size of a clique in some particular kinds of graphs. These graphs are regular and they are in fact a union of graphs from some association scheme. Let $\omega(\Gamma)$ be the maximum size of a clique of a graph $\Gamma$ .

Theorem (Delsarte): If $\Gamma$ is the graph of an association scheme with valency $k$ , and if $\lambda$ is a negative eigenvalue of $\Gamma$ , then

$\omega(\Gamma)\le 1-k/\lambda$ .

I will give a proof I’ve seen in one of Chris Godsil’s notes as it bypasses the usual theory on inner distribution vectors and the MacWilliams transform.

Proof: Suppose we have an association scheme $\mathcal{A}$ with primitive idempotents $J=E_0,E_1,\ldots,E_d$ and suppose $\Gamma$ is a graph for one of the relations of $\mathcal{A}$ , of order $n$ . Let $C$ be a clique of $\Gamma$ and let $\theta$ be an eigenvalue of $\Gamma$ with multiplicity $m_\theta$ . Let us denote by $E_\theta$ the primitive idempotent whose rowspace is the eigenspace corresponding to $\theta$ . Then the submatrix of $E_\theta$ with rows and columns indexed by the vertices of $C$ has the form

$\alpha I + \beta J.$

Since $E_\theta$ is positive semidefinite, the eigenvalues of $\alpha I + \beta J$ are non-negative. The constant row-sum value of $E_\theta$ is an eigenvalue, and so $\alpha + (|C| - 1)\beta$ is an eigenvalue and thus is non-negative. This implies that

$|C|\le 1-\alpha/\beta$ .

Since $\alpha I$ is the Hadamard product $I\circ E_\theta$ we have $n\alpha = \mathrm{Trace}(E_\theta) = m_\theta$ . Let $A$ be the adjacency matrix for $\Gamma$ . Since $AE_\theta = \theta E_\theta$ and $A\circ E_\theta = \beta A$ , we have

$\beta n k = \sum(\beta A) = \sum(A\circ E_\theta) = \mathrm{Trace}(AE_\theta) = \theta m_\theta$ . Therefore $\beta=\theta \alpha/k$ . Hence, if we consider all cliques and the least eigenvalue $\lambda$ , we have $\omega(\Gamma)\le 1-k/\lambda.$

$\square$

This bound doesn’t hold for all regular graphs, as we shall see.

Generalised quadrangles

Consider a generalised quadrangle of order $(s,t)$ and its collinearity graph $\Gamma$ . Then $\Gamma$ is regular of valency $s(t+1)$ and a maximal clique of $\Gamma$ is simply the set of points incident with some line. So $\omega(\Gamma)=s+1$ . The eigenvalues of $\Gamma$ are $s(t+1)$ , $s-1$ and $-t-1$ . Now $\Gamma$ is strongy regular and so is the graph of an association scheme, and Delsarte’s bound applies and is tight:

$\omega(\Gamma)\le 1-s(t+1)/(-t-1)=s+1$ .

Now consider what we get when we remove a line $\ell$ of $\Gamma$ . If $s\ge 2$ , then the biggest clique of $\Gamma-\ell$ is still the set of points of a line of the original generalised quadrangle. The valency of $\Gamma-\ell$ is $s(t+1)-1$ . So if Delsarte’s bound applies, then the least negative eigenvalue $\tau$ of $\Gamma-\ell$ satisfies $s+1\le 1-(s(t+1)-1)/\tau$ , and hence,

$\tau\ge 1/s-(t+1).$

However, by the theory of interlacing eigenvalues, we must have $\tau\le -(t+1)$ ; a contradiction.

Question

For what families of regular graphs does this bound hold?

5 thoughts on “When does Delsarte’s bound hold?”

Dima says:

May 28, 2012 at 4:40 am

I don’t understand the argument in the last sentence, as the minimal eigenvalue of an induced subgraph is always bigger than or equal to the minimal eigenvalue of the graph (by interlacing!).

By the way, is there a description of eigenvectors of collinearity graphs of GQs which correspond to eigenvalue s-1 ?

1. Gordon Royle says:
  
  May 30, 2012 at 10:39 am
  
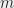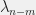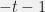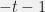  By “generalised interlacing”, deleting $m$ vertices from a graph alters the minimum eigenvalue from $\lambda_n$ to somewhere between $\lambda_{n-m}$ and $\lambda_n$ . As the original collinearity graph has got lots of eigenvalues equal to $-t-1$ (that is, more than $s+1$ ) the minimum eigenvalue of the graph after deleting the vertices of a line is still equal to $-t-1$ , and the bound fails.
  
  As for the eigenvectors of the collinearity graph, consider the following set: take two intersecting lines and put a weight of +1 on each point of the first line, -1 on each point of the second line, 0 on the point of intersection and 0 elsewhere. Unless I screwed up, this is an eigenvector with eigenvalue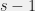 $s-1$ . I don’t know if this is all of them though.
  
John Bamberg says:

June 18, 2012 at 8:09 pm

There are heaps of eigenvectors with eigenvalue $s-1$ , they form a vector space! The ones that Gordon describes form a spanning set.

1. Dima says:
  
  July 5, 2012 at 12:47 am
  
  Thanks. Indeed, I meant to ask for a combinatorial description…
  
  1. John Bamberg says:
    
    July 9, 2012 at 8:57 pm
    
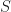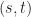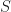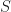    Yes, in a way there is. Let $S$ be a set of points of a GQ of order $(s,t)$ . Now consider the average valency of $S$ , that is, the average number of points $a$ of $S$ collinear with a given point of 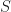$S$ . Then it can be shown that $a\le s-1+|S|/(s+1)$ , and if equality is attained, then 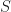$S$ is what is called a tight set of the GQ. If we let 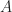$A$ be the collinearity matrix of the GQ, we have an equivalent definition of a tight set in terms of the characteristic vector of $S$ :
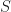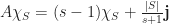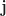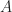    $A\chi_S=(s-1)\chi_S+ \frac{|S|}{s+1}\mathbf{j}$ where ${\mathbf{j}}$ is the all-ones vector. So $-(st+1)\chi_S-\frac{|S|}{s+1}\mathbf{j}$ is an eigenvector of $A$ with eigenvalue $s-1$ .