Generalised quadrangles II

In this post I wish to give a construction of some nonclassical generalised quadrangles, that is, ones other than ${\mathsf{H}(3,q^2),\mathsf{H}(4,q^2), \mathsf{W}(3,q),\mathsf{Q}(4,q),\mathsf{Q}^-(5,q)}$ and the dual of ${\mathsf{H}(4,q^2)}$ . These were discussed in the previous post.

The construction I will discuss is known as Payne derivation and is due to Stan Payne. It constructs new GQs from old ones.

Regular points

First I need to introduce some terminology and discuss the notion of a regular point. Let ${\mathcal{Q}}$ be a generalised quadrangle of order ${(s,t)}$ . Let ${x,y}$ be points of ${\mathcal{Q}}$ . We say that ${x}$ is collinear to ${y}$ if there is a line of the GQ containing both ${x}$ and ${y}$ . We usually denote this by ${x\sim y}$ and if ${x}$ and ${y}$ are not collinear we write ${x\not\sim y}$ . For a set ${S}$ of points let ${S^{\perp}}$ denote the set of points collinear with each element of ${S}$ . We say that a point ${x}$ is incident with a line ${\ell}$ if ${\ell}$ contains ${x}$ . Again we denote this by ${x\sim \ell}$ .

Now suppose that ${x,y}$ are two points such that ${x}$ is not collinear with ${y}$ . For each line ${\ell}$ incident with ${x}$ , since ${y}$ is not on ${\ell}$ there is a unique point on ${\ell}$ incident with ${y}$ . Since ${x}$ lies on ${t+1}$ lines, it follows that ${\{x,y\}^{\perp}}$ has size ${t+1}$ . Moreover, for each ${u,v\in\{x,y\}^{\perp}}$ we have that ${u}$ is not incident with ${v}$ , otherwise ${x,u,v}$ would be a triangle in the geometry. Thus ${\{u,v\}^\perp}$ has size ${t+1}$ . Hence ${\{x,y\}^{\perp\perp}}$ has size at most ${t+1}$ . Note that ${x,y\in\{x,y\}^{\perp\perp}}$ so we in fact have that ${2\leq |\{x,y\}^{\perp\perp}|\leq t+1}$ . If ${\{x,y\}^{\perp\perp}=t+1}$ for all points ${y}$ not collinear with ${x}$ we say that ${x}$ is a regular point.

I will now look at what actually happens in some of the classical GQs. In ${\mathsf{W}(3,q)}$ , a GQ of order ${(q,q)}$ , let ${e_1=(1,0,0,0)}$ , ${e_2=(0,1,0,0)}$ , ${f_1=(0,0,1,0)}$ and ${f_2=(0,0,0,1)}$ . (I will use the alternating form described in the previous post.) Then ${e_1\not\sim f_1}$ . Moreover, ${e_1^{\perp}=\langle e_1,e_2,f_2\rangle}$ while ${f_1^{\perp}=\langle e_2,f_1,f_2\rangle.}$ Thus ${\{e_1,f_1\}^{\perp}=\langle e_2,f_2\rangle}$ and ${\{e_1,f_1\}^{\perp\perp}=\langle e_1,f_1\rangle}$ . This 2-space contains ${q+1}$ points and so the upper bound can be met. Since the automorphism group of ${\mathsf{W}(3,q)}$ is ${\mathrm{P}\Gamma\mathrm{Sp}(4,q)}$ , which has rank 3 on the points of the GQ, it is transitive on pairs of noncollinear points and so we have ${\{x,y\}^{\perp\perp}}$ has size ${t+1}$ for all pairs of noncollinear points ${x}$ and ${y}$ . Thus all points of ${\mathsf{W}(3,q)}$ are regular.

In ${\mathsf{Q}(4,q)}$ , for ${q}$ odd, we can choose a basis ${\{e_1,e_2,f_1,f_2,u\}}$ of the underlying 5-dimensional vector space such that the quadratic form ${Q}$ evaluates to 0 on each ${e_i}$ and ${f_i}$ but ${Q(u)=1}$ . Moreover, ${B(e_i,e_j)=B(f_i,f_j)=B(e_i,u)=B(f_i,u)=0}$ while ${B(e_i,f_i)=1}$ . Then ${e_1\not\sim f_1}$ and ${\{e_1,f_1\}^{\perp}=\langle e_2,f_2,u\rangle}$ and ${\{e_1,f_1\}^{\perp\perp}=\langle e_1,f_1\rangle}$ . The totally singular points in this 3-space are ${\langle e_1\rangle}$ and ${\langle f_1\rangle}$ , and so in the GQ, ${\{e_1,f_1\}^{\perp\perp}}$ has size 2. Thus the lower bound can hold. In fact, since the automorphism group of this GQ has rank 3 we have ${\{x,y\}^{\perp\perp}}$ has size 2 for all pairs ${x,y}$ of noncollinear points.

In ${\mathsf{H}(4,q^2)}$ , a GQ of order ${(q^2,q^3)}$ , we can choose a basis ${\{e_1,e_2,f_1,f_2,u\}}$ such that ${B(e_i,e_i)=B(f_i,f_i)=B(e_i,f_j)=B(e_i,u)=B(f_i,u)=0}$ and ${B(e_i,f_i)=1}$ . Then ${\{e_1,f_1\}^{\perp\perp}=\langle e_1,f_1\rangle}$ . The only totally isotropic points in this two space are ${\langle e_1\rangle}$ and ${\langle \lambda e_1+f_1\rangle}$ where ${\lambda+\lambda^q=0}$ . There are ${q}$ such values of ${\lambda}$ and so in the GQ, ${\{e_1,f_1\}^{\perp\perp}}$ has size ${q+1<q^3+1}$ .

Payne’s construction

Let ${\mathcal{Q}}$ be a generalised quadrangle of order ${(s,s)}$ . Given a regular point ${x}$ , we can construct a new generalised quadrangle ${\mathcal{Q}^x}$ whose points are the points of ${\mathcal{Q}}$ not collinear with ${x}$ . The lines come in two flavours:

(i) the lines of ${\mathcal{Q}}$ not incident with ${x}$ (if you like to think of the lines as subsets of points then you need to remove any points collinear with ${x}$ from such lines),
(ii) the sets ${\{x,y\}^{\perp\perp}}$ where ${y}$ is not collinear with ${x}$ . (again, need to remove ${x}$ if we wish to think of subsets of points.)

Incidence is then the incidence inherited from ${\mathcal{Q}}$ .

This new geometry is a generalised quadrangle. Those interested in a proof of this should consult the original paper `Nonisomorphic generalised quadrangles’ of Payne or the book `Finite generalised quadrangles’ by Payne and Thas.

The lines of the first type are incident with ${s+1}$ points of ${\mathcal{Q}}$ and by the GQ property, exactly one of these points is incident with ${x}$ . Hence lines of the first type are incident with ${s}$ points. Also, as ${x}$ is a regular point, each line ${\{x,y\}^{\perp\perp}}$ contains ${s+1}$ points of ${\mathcal{Q}}$ . The only such point incident with ${x}$ is ${x}$ itself so lines of the second type also are incident with ${s}$ points.

Given a point ${y}$ of ${\mathcal{Q}^x}$ , it is incident with ${s+1}$ lines of the orginal GQ and as ${y}$ is not collinear with ${x}$ none of these lines contains ${x}$ and so are all lines of ${\mathcal{Q}^x}$ . Moreover, ${y}$ is incident with the line ${\{x,y\}^{\perp\perp}}$ . If ${y'\in\{x,y\}^{\perp\perp}\backslash\{x\}}$ then ${\{x,y'\}^{\perp}=\{x,y\}^{\perp}}$ and so ${\{x,y\}^{\perp\perp}=\{x,y'\}^{\perp\perp}}$ . Hence ${\{x,y\}^{\perp\perp}}$ is the unique line of the second type containing ${y}$ . Thus each point of ${\mathcal{Q}^x}$ is incident with ${s+1}$ lines. So our new GQ has order ${(s-1,s+1)}$ .

Now for what generalised quadrangles can we use this construction?

So far the only GQs of order ${(s,s)}$ that we have seen are ${\mathsf{W}(3,q)}$ and ${\mathsf{Q}(4,q)}$ . We saw above that all points of ${\mathsf{W}(3,q)}$ are regular but none of the points of ${\mathsf{Q}(4,q)}$ are regular. Applying Payne derivation to ${\mathsf{W}(3,q)}$ we obtain a generalised quadrangle of order ${(q-1,q+1)}$ . These GQs has been previously obtained by an alternative construction by Ahrens and Szekeres, and by Marshall Hall in the case where ${q}$ is even.

Remember that we also obtain a GQ of order ${(q+1,q-1)}$ from the dual.

Now for ${q=3}$ we obtain a generalised quadrangle of order ${(2,4)}$ . We have already seen the generalised quadrangle ${\mathsf{Q}^-(5,2)}$ which also has order ${(2,4)}$ . In fact these two GQs are isomorphic.

For ${q=4}$ , the full automorphism group of our new GQ of order ${(3,5)}$ is ${2^6:(3.A_6.2)}$ , which acts transitively on both the points and lines of the GQ.

For ${q\geq 5}$ it was shown by Grunhöfer, Joswig and Stroppel that the full automorphism group of the GQ of order ${(q-1,q+1)}$ obtained by Payne derivation from ${\mathsf{W}(3,q)}$ using the regular point ${x}$ is just ${\mathrm{P}\Gamma\mathrm{Sp}(4,q)_x}$ , that is the stabiliser of ${x}$ in the automorphism group of the original GQ. This group is transitive on points but will have two orbits on the lines corresponding to the two types.

There are other GQs to which we can apply Payne derivation but we haven’t introduced them yet and so they will have to be the subject of another post.

Author: Michael Giudici

Mathematician View all posts by Michael Giudici

3 thoughts on “Generalised quadrangles II”

Anurag Bishnoi says:

December 9, 2013 at 9:11 pm

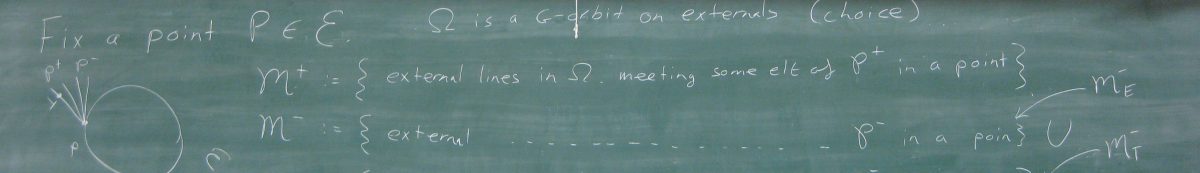
There is a typo in “we have that {u} is not incident with {y}, “. It should be v instead of y. (Regular points)

1. Michael Giudici says:
  
  December 10, 2013 at 8:34 am
  
  Thanks, I have corrected it.
  
  1. Anurag Bishnoi says:
    
    December 12, 2013 at 11:22 am
    
    No problem.
    
    Thanks for these posts. Being a newcomer to finite geometry myself, these are quite helpful. I hope you can write something similar summarising the basic constructions of known generalized hexagons and octagons (the only other non-trivial finite generalized polygons).