AMSI Summer Vacation Scholarship

Below is a guest blog post of Melissa Lee, who took part in a six-week summer vacation research project supported by the Australian Mathematical Sciences Institute.

 

Hi everyone! My name is Melissa Lee and I’ve recently started honours with John and Dr. Eric Swartz here at UWA. This past summer I have been working with John on an AMSI Vacation Research Scholarship. My AMSI VRS project was based on looking at structures embedded in an affine space by viewing them in terms of a game called SET.

The game SET was invented by Marsha Falco, a geneticist at Cambridge in 1974. She was studying epilepsy in German Shepherds and drew symbols on index cards to represent some of the different genes she was studying. She developed this concept into a game, which was eventually placed on the market in 1990. There are 81 SET cards, each with four different traits – colour, shape, number and shading. The aim of SET is to match three cards by having each of the four traits either all the same over the three cards or all different.

The first row of cards form a SET, but the second row do not.

Mathematicians soon discovered that this game SET could be modelled as AG(4,3) – an affine space of points and lines. Each point is represented by four ternary coordinates and there are three points on every line. Since each point is represented by four coordinates, this means that this affine space is four-dimensional — hard to visualise for even the greatest mathematicians! However, if we take each dimension as one of the four traits of SET, this affine space becomes much easier to think about. Using this mapping, we have that each of the points of the affine space are SET cards, and each of the lines are the SETs that we mentioned earlier.

Many mathematicians before me, particularly Joseph Thas, have done a wide variety of research on the different interesting mathematical structures we can embed in affine spaces like AG(4,3). However, many of these concepts have never before been considered in the context of SET.

Generalised quadrangles are a good example. A generalised quadrangle of order is an set of points and lines such that:

1. Any two points are on at most one line together.
2. Every point is on lines.
3. Every line has points on it.
4. For any point that is not on a line , there is a unique point on on a line with .

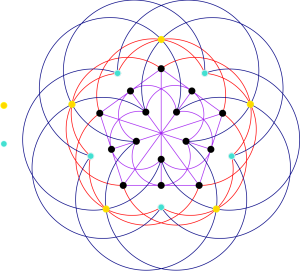
In AG and thus SET, we can find three non-trivial generalised quadrangles. We focus mainly on two of these — GQ and GQ. We can look at these generalised quadrangles in the context of SET below.

GQ(2,2) (purple) embedded in GQ(2,4) in a SET card representation.

It just so happens that GQ (also sometimes called ‘the doily’) can be embedded or ‘found’ in GQ , the unique generalised quadrangle with these parameters (evident in the figure above). This allows us to find relative hemisystems of points using these two generalised quadrangles.

Relative hemisystems are quite a new topic in finite geometry. They were introduced in 2011 by Penttila and Williford as an extension of hemisystems, which has been quite a hot topic in finite geometry over the past few years. To find a relative hemisystem, we take the points and lines that make up the doily out of GQ(2,4). We then try and take points in the remaining structure such that each of the remaining lines has exactly one point on it. It turns out that we can find just two relative hemisystems this way, each consisting of six points.

An illustration of GQ(2,4) with the relative hemisystems highlighted in gold and blue.

A natural structure in our affine space that we can look at in SET is caps. Caps are the largest set of points such that no three are on the same line — or, in terms of SET — the maximum number of SET cards we can choose before we must have a SET. It is well known that in the affine space that SET represents, the largest cap is of size 20 (this has been stated in terms of SET by various authors including Monash University’s Dr. Norm Do). What is even more interesting is that when we consider the generalised quadrangles we found earlier in SET, we find that the size of the maximal cap is 17, which is very large considering GQ(2,4) only contains a third of the 81 cards of SET.

 

The SET cards corresponding to a maximal cap in GQ(2,4) and their corresponding positions on the illustration.

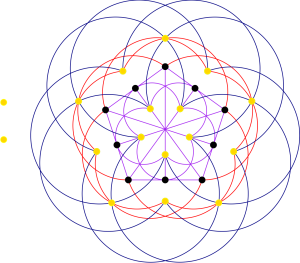
However, as we can see from the SET cards in the third row, the maximal cap of contains SETs. This doesn’t contradict the definition of a cap because the line corresponding to that SET isn’t included in the lines of . However, we find that the nice definition of a cap in terms of SET loses meaning when we restrict it to our generalised quadrangle.

Throughout this project, I have been amazed by how nicely we can visualise this abstract affine space in terms of a fun game like SET. We can see many beautiful symmetries and patterns arise and infer the impact of group theory in finite geometry. It would be interesting in future to see whether we can somehow ‘give back’ to SET. That is, determining whether we can modify the normal rules of SET so that the concept of a maximal cap over a generalised quadrangle gains meaning and to see whether we can produce these other interesting structures in the game. I’d like to thank John for giving up so much of his time to teach me about the basics of finite geometry for this project and helping me prepare to speak at the CSIRO Big Day In conference. I’d also like to thank Gordon for his support and AMSI for their sponsorship.